Área Abaixo da Curva ROC
Em busca de uma intuição
Em todas as competições do Kaggle que eu participei e que envolviam classificações binárias, a métrica de avaliação foi a Área Abaixo da Curva ROC (AUC). Por conta disso, eu fui procurar por uma explicação para essa métrica.
Um dos melhores links que eu encontrei foi esse, que contém ilustrações que facilitam a compreensão. Mas eu ainda não estava satisfeito, pois o assunto ainda não tinha chegado na minha intuição com clareza.
Eu continuei buscando e então me deparei com esta resposta no StackExchange:
A AUC de um classificador é a probabilidade de que um exemplo positivo aleatório seja pontuado acima de um exemplo negativo aleatório.
Bingo! Finalmente uma explicação que chegou à minha compreensão. Mas e aí, por que isso é verdade? Eu busquei várias explicações para esse fato mas não consegui entender direito com nenhuma delas isoladamente. Portanto, decidi escrever este texto após mastigar bastante sobre o assunto.
Vamos então definir matematicamente a AUC. Seja \(f\) a função do classificador, que recebe uma entrada \(x\) e retorna a probabilidade \(f(x)\) de \(x\) ser um caso positivo. Ao definirmos um valor \(T\) para que o classificador responda sim quando \(f(x) > T\) ou não quando \(f(x) < T\), normalmente cometemos erros acusando falsos positivos e falsos negativos. A taxa de verdadeiros positivos (\(TPR\)) é a razão entre a quantidade de casos positivos para os quais o classificador disse sim e a quantidade de casos positivos. A taxa de falsos positivos (\(FPR\)) é a razão entre a quantidade de casos negativos para os quais o classificador disse sim e a quantidade de casos negativos. Assim, a curva ROC é definida pelos pontos \((FPR, TPR)\), onde \(T \in (-\infty, \infty)\). A AUC está ilustrada na Figura 1.
 Figura 1
Figura 1
Formalmente, consideramos \(TPR\) como uma função de \(FPR\) e integramos de 0 a 1 para calcularmos a área:
\[\textrm{AUC} = \int_0^1 TPR(FPR) dFPR \hspace{1cm}(1)\]No entanto, \(TPR\) e \(FPR\) são funções de \(T\). Sendo \(FPR'\) a derivada de \(FPR(T)\) em relação a \(T\), temos que \(dFPR = FPR'(T)dT\). Antes de fazermos a substituição de variável na integral, note que:
- \(FPR(\infty) = 0\), pois nenhum caso é classificado como positivo
- \(FPR(-\infty) = 1\), pois todos os casos são classificados como positivos
Substituindo na Equação 1, obtemos:
\[\textrm{AUC} = \int_{\infty}^{-\infty} TPR(FPR(T)) FPR'(T) dT\]Seja \(x^+\) uma variável aleatória discreta que assume valores dentre os casos positivos com distribuição uniforme. Denotemos por \(f(x^+)\) a variável aleatória contínua resultante da aplicação da função \(f\) em cada caso positivo \(x^+\). A taxa de verdadeiros positivos pode ser entendida como a probabilidade de que \(f(x^+)\) seja maior que \(T\). Além disso, trocando os limites da integral e invertendo o sinal do integrando, obtemos:
\[\textrm{AUC} = \int_{-\infty}^{\infty} P(f(x^+) > T) [-FPR'(T)] dT\]Substituindo \([-FPR'(T)]\) pela derivada de uma primitiva estratégica:
\[\textrm{AUC} = \int_{-\infty}^{\infty} P(f(x^+) > T) \left[ \frac{d}{dT}(1 - FPR(T)) \right] dT\]Complementar à taxa de falsos positivos, temos a taxa de verdadeiros negativos (\(TNR\)), que é a razão entre a quantidade de casos negativos para os quais o modelo respondeu não e a quantidade de casos negativos. Assim, \(TNR(T) = 1-FPR(T)\):
\[\textrm{AUC} = \int_{-\infty}^{\infty} P(f(x^+) > T) TNR'(T) dT \hspace{1cm}(2)\]Agora, similarmente a \(x^+\) e \(f(x^+)\), definamos \(x^-\) e \(f(x^-)\). Seja também \(p\) a função de densidade probabilística da variável aleatória \(f(x^-)\). Observemos então a relação entre \(p\) e \(TNR(T)\) na Figura 2.
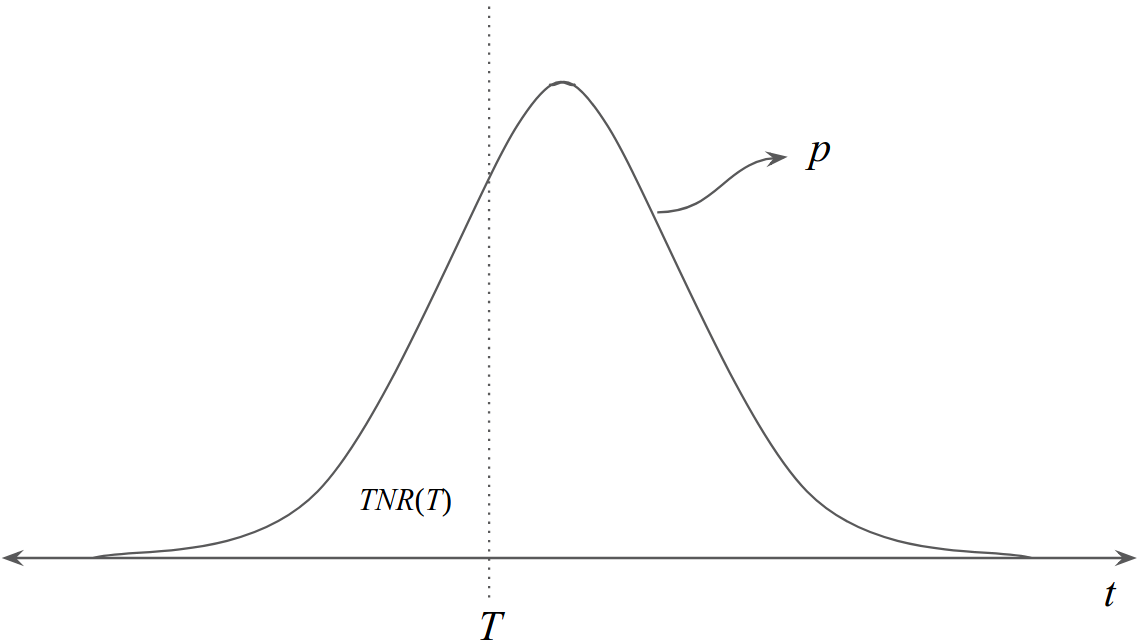 Figura 2
Figura 2
Logo, \(TNR(T)\) pode ser calculado com a seguinte integral:
\[TNR(T) = \int_{-\infty}^{T} p(t) dt\]Pelo Teorema Fundamental do Cálculo, temos que TNR′(T) = p(T). Substituindo na Equação 2, obtemos:
\[\textrm{AUC} = \int_{-\infty}^{\infty} P(f(x^+) > T) p(T) dT \hspace{1cm}(3)\]Agora estamos quase no final. Para o último passo, vamos fazer uma visita a um resultado da Estatística. Sejam \(X\) e \(Y\) duas variáveis aleatórias contínuas. Nós podemos calcular \(P(X > Y)\) quebrando \(Y\) em valores \(y\), cada um ocorrendo com probabilidade expressa pela função de densidade probabilística de \(Y\), \(q\):
\[P(X > Y) = \int_{-\infty}^{\infty} P(X > y) q(y) dy \hspace{1cm}(4)\]Como \(p\) é a função de densidade probabilística da variável aleatória \(f(x^-)\), podemos aplicar o resultado da Equação 4 na Equação 3:
\[\textrm{AUC} = P(f(x^+) > f(x^-)) \hspace{1cm}\blacksquare\]Interessante! Vamos fazer uns testes?
Experimentos
Vamos instanciar pontuações dadas para 4 casos positivos e 6 negativos nas listas
pos e neg, respectivamente.
from sklearn.metrics import roc_auc_score
truth = [1., 1., 1., 1., 0., 0., 0., 0., 0., 0.]
score = [.7, .7, .2, .4, .2, .3, .1, .5, .2, .1]
pos, neg = [], []
for i in range(len(truth)):
if truth[i] > 0:
pos.append(score[i])
else:
neg.append(score[i])
Agora comparemos o resultado obtido com a função roc_auc_score da biblioteca
scikit-learn com o resultado de um
experimento probabilístico, no qual verificamos quantos pares de casos positivos
e negativos atendem à condição de que a pontuação dada ao caso positivo seja maior
que à dada ao negativo. É importante estarmos atentos para os pares cujas pontuações
são iguais, pois, em aproximadamente metade das possíveis ordenações segundo
as pontuações, o caso positivo estará elencado acima do negativo. Portanto, para
estes casos, consideraremos que pares assim contribuem para a contagem com apenas
0.5.
Vejamos o resultado para 1 milhão de pares aleatórios.
from random import choice
N, count = 1_000_000, 0
for _ in range(N):
positive = choice(pos)
negative = choice(neg)
if positive > negative:
count += 1
elif positive == negative:
count += .5
print('scikit-learn:', roc_auc_score(truth, score))
print('our experiemnt:', count/N)
Resultados:
scikit-learn: 0.8333333333333333
our experiemnt: 0.833478
Bem próximo, mas um tanto demorado. Vamos ser mais inteligentes.
Existem 6\(\times\)4=24 pares possíveis. Vejamos qual a proporção dos pares que atendem à condição.
count = 0
for p in pos:
for n in neg:
if p > n:
count += 1
elif p == n:
count += .5
print('scikit-learn:', roc_auc_score(truth, score))
print('our experiemnt:', count/( len(pos)*len(neg) ))
Resultados:
scikit-learn: 0.8333333333333333
our experiemnt: 0.8333333333333334
Agora sim, ainda mais próximo e mais rápido!
Nota: a implementação oficial não faz uso destes loops de contagem apresentados aqui.
Breve conclusão
Por este significado da AUC, eu a entendo como uma ótima métrica para quando quisermos, por exemplo, construir filas de prioridades segundo as saídas probabilísticas de classificadores binários.
Bibliografia
- Bamber, D., “The area above the ordinal dominance graph and the area below the receiver operating graph”. Journal of Mathematical Psychology, 12, 387–415, 1975.