Divisão e conquista para predição

20/12/2017

Quando praticamos aprendizagem de máquina, idealmente gostaríamos de encontrar uma função capaz predizer qualquer entrada desconhecida de forma confiável, mas nem sempre isso é possível. Nestes casos, uma estratégia possível é particionar o espaço amostral para encontrarmos alguns clusters nos quais nossos modelos de aprendizado são capazes de obter resultados mais acurados.

Neste artigo apresentarei uma forma de implementar a divisão e conquista utilizando o algoritmo \(k\)-means. Mas antes, façamos uma breve revisão.

\(k\)-means

\(k\)-means é um algoritmo de clusterização, ou seja, sua utilidade é agrupar elementos semelhantes. Sua lógica é a seguinte:

Inicia-se com \(k\) pontos aleatórios distribuidos ao longo do espaço amostral, denominados centroides. Cada centroide \(c\) é o centro do conjunto vazio \(S_c\)
Para cada elemento \(e\) do conjunto de treinamento, verifica-se a distância de \(e\) para cada centroide e adiciona-se \(e\) a \(S_{c_p}\), onde \(c_p\) é o centroide mais \(p\)róximo de \(e\)
Para cada conjunto \(S_i\), recalcula-se o centroide \(i\)
Repete-se a partir do passo 2 até que os centroides se estabilizem

Estratégia de treinamento

Definamos um parâmetro \(k_{\max}\) e iteramos \(k\) de \(1\) até \(k_{\max}\)
Para cada \(k\):

2a. Executamos o algoritmo \(k\)-means, resultando em \(k\) clusters. É importante que não incluamos na computação dos clusters a coluna relacionada à variável que queremos predizer, pois estes valores não estarão disponíveis no momento da inferência

2b. Em cada cluster, computamos a função de predição e avaliamos sua acurácia. A função de predição pode ser computada utilizando métodos já conhecidos como regressões logísticas, redes neurais etc. Sejam:
- \(f_{k_i}\) a função de predição do \(i\)-ésimo cluster dentre os \(k\) e
- \(A(f_{k_i})\) a acurácia de \(f_{k_i}\)
2c. Obtemos a média \(\mu_k\) e o desvio padrão \(\sigma_k\) das acurácias das funções de predição, levando em consideração a cardinalidade de cada cluster

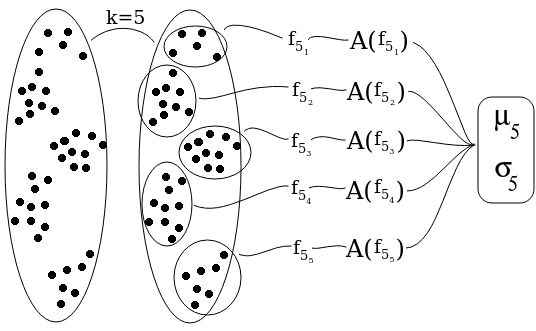Divisão (\(k\)-means) e conquista (\(f_{k_{1..k}}\))

Agora podemos avaliar quais valores de \(k\) são interessantes. Estamos interessados em dois cenários:

Valores altos de \(\mu_k\) indicam que, em média, as funções de predição tiveram um bom desempenho nos clusters obtidos
Valores médios de \(\mu_k\) e valores altos de \(\sigma_k\) indicam que, para alguns clusters, as funções de predição tiveram um bom desempenho

Estratégia de predição

Ao escolhermos o valor de \(k\) que melhor julgamos segundo \(\mu_k\) e \(\sigma_k\), estaremos considerando os respectivos centroides \(c_1\), …, \(c_k\) resultantes da execução do \(k\)-means.

Seja \(e\) uma entrada para a qual queremos fazer a predição em questão. Calculamos então as distâncias \(d_1\), …, \(d_k\) de \(e\) até \(c_1\), …, \(c_k\), respectivamente.

Façamos então uma avaliação fuzzy da pertinência de \(e\) em relação a \(S_1\), …, \(S_k\). Supondo que o grau de pertinência é inversamente proporcional à distância até o centroide, chegamos à seguinte fórmula para a predição de \(e\) segundo o particionamento em \(k\) clusters:

\[f_k(e) = \frac{\sum_\limits{i=1}^k \frac{1}{d_i} \times f_{k_i}(e)}{\sum_\limits{i=1}^k \frac{1}{d_i}},\]

com o devido cuidado nos casos em que \(d_i = 0\).

Quando \(k = 1\), obtemos o resultado sem a estratégia de divisão e conquista. Este resultado será avaliado frente aos resultados obtidos com outros valores de \(k\).

Variações

Usar um coeficiente \(\lambda\) para definirmos o quanto a distância até os centroides pesa na avaliação de \(e\), de modo que quanto maior \(\lambda\), mais a predição de \(f_k(e)\) será influenciada pelos clusters mais próximos de \(e\). A fórmula resultante seria:

\[f_k(e) = \frac{\sum_\limits{i=1}^k \frac{1}{d_i^\lambda} \times f_{k_i}(e)}{\sum_\limits{i=1}^k \frac{1}{d_i^\lambda}}\]

Simplificar o modelo, abandonando completamente a abordagem fuzzy e avaliando \(e\) puramente com a função de predição do cluster mais próximo, com alguma resolução para os casos de empate

Avaliando o custo

A grande desvantagem desta estratégia é o custo computacional. O conjunto de treinamento precisa ser particionado várias vezes e, para cada particionamento, é necessário executar o algoritmo de aprendizagem. Mas poder computacional é algo escalável, principalmente com as tecnologias que estão surgindo, como por exemplo a biblioteca TensorFlow.

Além disso, a depender do método de aprendizagem escolhido, a computação de funções de predição pode ser mais eficiente se replicada em partições do que se executada no conjunto de treinamento inteiro. Exemplos disso são os métodos que envolvem invesões de matrizes, cujos algoritmos têm complexidades mais altas que \(O(n^{2.37})\) até o momento.